"A mind stretched by a new idea can never go back to its original dimensions."
- Oliver Wendell Holmes -
3D Simulations
In order explain ether theory, I had to find an appropriate 3D simulation software application that enabled me to construct a realistic representation of foamy ether. I wanted to create simulations that would demonstrate the various structures and activities of ether. I managed to find a 3D software package, with a built in java like scripting language, that allowed me to manipulate objects accordingly. This allowed me to create simulations that demonstrate various physical phenomena (i.e. gravity, electromagnetic waves, etc.). This way, no knowledge of mathematics is required on the part of the reader. Everything is explained by using simulations and snapshots of simulations.
Once I became proficient at using the software, I was pleasantly surprised at how easily it could be modeled to simulate actual physical phenomena. This gave me great confidence in the foamy ether model.
To make a 3D model of foamy ether, I created a 3D array of spheres (or nodes). These nodes are connected together with neighbouring nodes by a spring and damper pair to form an array of bubbles or cells (see Figure 2). These springs are stretched to mimic the properties of stretched foamy ether. I then had to set the outer nodes as stationary, otherwise the whole model would collapse because of the tension on the springs. My working model was much larger (about 60X60X60, the maximum array size the RAM in my computer could accommodate).
The size of a bubble (or cell) is determined by the distance between nodes, one Planck Length, or 1.616 X 10-35 meters. (This is no coincidence - more on that later).

Figure 2
After creating a 60X60X60 array, I found that it was too cluttered, which made it impossible to see its centre. Fortunately, the software allowed me to make portions of the array invisible. That enabled me to create a two dimensional slice of the 3D array (just like an MRI provides a series of two dimensional image slices of a three dimentional human body). This is shown below. In Figure 3a, the springs and nodes are visible. In Figure 3b, only the springs are visible. (In some simulations every fifth set of springs is colored in blue to make the distortions more clear).

Figure 3a
Figure 3b
This array of springs and dampers also works extremely well in modeling Indra's Net. Figure 3c shows a simulation of how moving one node (or pearl) creates a ripple effect in the tightly stretched, elastic like net, causing all other nodes to adjust.
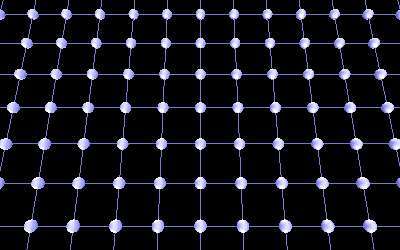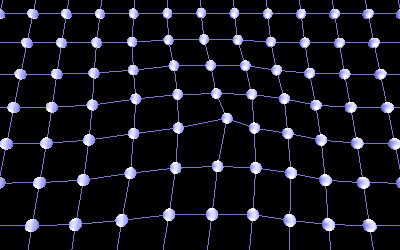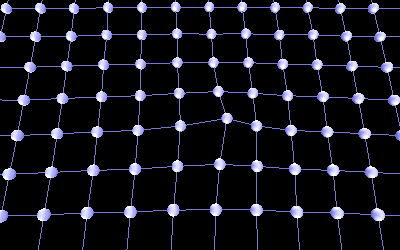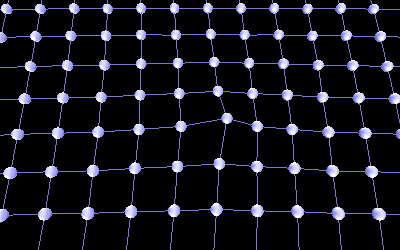
Figure 3c Indra's Net
More recently, I built a model of foamy ether using hexagons instead of squares (Figure 3d). This makes the model a little more accurate (and isotropic), although it didn't make much of a difference in the simulations.

Figure 3d